Resum de Haskell

Transparències de laboratori: https://www.cs.upc.edu/~jpetit/Haskell/#1

---

LAB 1: Recursivitat

Exercisis proposats:

• P77907
• P25054
• P29040

---

LAB 2: Funcions de ordre superior

map aplica una funció desitjada a cada element de una llista.

map (*2) [1..4]
-- [2, 4, 6, 8]

zipWith combina dues llistes en una mitjançant una operació desitjada

-- funcio que combina dues llistes amb la suma dels seus respectius elements
a = zipWith (+) x y

foldl i foldr defineixen operadors, ja sigui per la dreta o per l’esquerra, que s’apliquen entre cada element de les llistes, ja sigui de dreta a esquerra o viceversa, i que dona com a resultat un element.

-- l'element es de tipus corresponen a l'operador i els elements de la llista. Aquesta funció aplica l'operador (++) per la dreta a totes les subllistes. Per tant, retorna un allista amb tots els elements concatenats.
flatten :: [[Int]] -> [Int]
flatten = foldr (++) []

filter retorna una llista amb els element que compleixen un predicat concret.

-- aquesta funció retorna una llista de tots els elements parells de a
filter (\x -> mod x 2 == 0) a

iterate genera una llista infinita de elements. iterate f x = [x, f(x), f(f(x)), ...]

-- Aquesta funció genera una llista infinita de les potències de 2
powersOf2 :: [Int]
powersOf2 = iterate (* 2) 1

Exercisis proposats:

P93632.hs

-- 1. Implement a function eql :: [Int] -> [Int] -> Bool that tells wether two lists of integers are equal.
eql :: [Int] -> [Int] -> Bool
eql a b
  | length a == length b = and $ zipWith eql' a b
  | otherwise = False
  where
    eql' :: Int -> Int -> Bool
    eql' x y = x == y

-- 2. Implement a function prod :: [Int] -> Int that returns the product of a list of integers.
prod :: [Int] -> Int
prod = foldl (*) 1

-- 3. Implement a function prodOfEvens :: [Int] -> Int that returns the product of all even numbers of a list of integers.
prodOfEvens :: [Int] -> Int
prodOfEvens a = prod $ filter (\x -> mod x 2 == 0) a

-- 4. Implement a function powersOf2 :: [Int] that generates the list of all the powers of 2.
powersOf2 :: [Int]
powersOf2 = iterate (* 2) 1

-- 5. Implement a function scalarProduct :: [Float] -> [Float] -> Float that returns the dot product of two lists of float numbers with the same size.

scalarProduct :: [Float] -> [Float] -> Float
scalarProduct a b = sum $ zipWith (*) a b

---

LAB 3: Llistes per comprensio i avaluacio mandrosa

Les llistes per comprensio s’assemblen al llenguatge matematic, i es creen amb definicions. Segueixen el format de [valor | condicions i definicions]. Les definicions diuen com son les variables que farem servir, i les condicions les filten.

Exemples

myMap f a = [f x | x <- a] redefineix la funcio map com una llista en la que la variable x pren tots els valors de a i el valor que resulta es calcula pasant aquest valor a una funcio f desitjada.

myFilter cond a = [x | x <- a, cond x]

factors n = [x | x <- [1 .. n], mod n x == 0]

Exercicis proposats

P98957.hs

-- Generate the sequence of ones [1,1,1,1,1,1,1,1,…].
ones :: [Integer]
ones = 1 : ones

-- Generate the sequence of the natural numbers [0,1,2,3,4,5,6,7…].
nats :: [Integer]
nats = 0 : map (+ 1) nats

-- Generate the sequence of the integer numbers [0,1,−1,2,−2,3,−3,4…].
ints' :: Integer -> Integer
ints' x
  | x > 0 = -x
  | x <= 0 = -x + 1

ints :: [Integer]
ints = 0 : map ints' ints

-- Generate the sequence of the triangular numbers: 0,1,3,6,10,15,21,28,…].
triangulars :: [Integer]
triangulars = scanl (+) 0 $ tail nats

-- Generate the sequence of the factorial numbers: [1,1,2,6,24,120,720,5040,…].
factorials :: [Integer]
factorials = scanl (*) 1 $ tail nats

-- Generate the sequence of the Fibonacci numbers: [0,1,1,2,3,5,8,13,…].
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)

-- Generate the sequence of prime numbers: [2,3,5,7,11,13,17,19,…].
isPrime :: Integer -> Bool
isPrime 1 = False
isPrime n = isPrime' 2
  where
    isPrime' :: Integer -> Bool
    isPrime' d
      | d == n = True
      | mod n d == 0 = False
      | otherwise = isPrime' (d + 1)

primes :: [Integer]
primes = filter isPrime (drop 2 nats)

---

LAB 5: Functor, Applicative i Monad

Functor:

• Functor és una classe de tipus que representa una operació de mapeig sobre un tipus contenedor.
• Proporciona una única funció anomenada fmap (o <$>) que pren una funció i un valor Functor i aplica la funció als valors dins del Functor, mantenint l’estructura.
• La classe de tipus Functor permet elevar funcions per a treballar amb valors dins del contenidor sense desempaquetar-los explícitament.
• Exemples de Functors en Haskell són les llistes, Maybe i IO.

Applicative:

• Applicative és una classe de tipus que amplia les capacitats del Functor.
• Proporciona una funció anomenada pure que encapsula un valor en el contexte Applicative.
• També introdueix un operador <*> (o ap) que pren una funció encapsulada en el contexte Applicative i l’aplica als valors encapsulats en el mateix contexte.
• Això permet aplicar funcions amb múltiples arguments a valors Applicative d’una manera convenient.
• Exemples d’Applicatives en Haskell són Maybe i les llistes.

Monad:

• Monad és una altra classe de tipus que es basa en Applicative i Functor.
• Proporciona una manera de seqüenciar càlculs mitjançant l’ús de l’operador >>= (bind).
• Monad permet combinar càlculs que depenen de resultats anteriors enllaçant automàticament els valors intermedis.
• També proporciona la funció return per encapsular un valor en el contexte Monad.
• Exemples de Monads en Haskell són Maybe, IO i les llistes.

Exercicis Proposats:

P87082.hs

-- implementacio llegint per linea
main :: IO ()
main = do
    linea <- getLine
    let paraules = words linea
    let nom = paraules !! 0
    if nom /= "*" then do
        let imcCalculat = imc (read (paraules !! 1) :: Float) (read (paraules !! 2) :: Float)
        let resultat = imcAvaluarResultat imcCalculat
        putStrLn $ nom ++ ": " ++ resultat
        main
    else 
        return ()


-- funcio de IMC, donats dos floats saber el imc
imc :: Float ->  Float -> Float
imc p a = p / (a*a)

-- funcio de avaluacio, donat l'IMC saber l'string que identifica el resultat
imcAvaluarResultat :: Float -> String
imcAvaluarResultat x
    | x < 18 = "underweight"
    | x < 25 = "normal weight"
    | x < 30 = "overweight"
    | x < 40 = "obese"
    | otherwise = "severely obese"

---

LAB 6: Entrada i sortida

Resum IO:

Per a entendre la entrada i sortida, que pot semblar algo molt sequencial, hem de pensar en el seguent exemple: Definim una estructura data World de la seguent manera:

data World = ... -- descripció del món
myGetChar :: World -> (World, Char)
myPutChar :: Char -> World -> (World, ())
myMain :: World -> (World, ())
myMain w0 = let (w1, c1) = myGetChar w0
                (w2, c2) = myGetChar w1
                (w3, ()) = myPutChar c1 w2
                (w4, ()) = myPutChar c2 w3
            in  (w4, ())

Podem veure que la funcio myGetChar es una funcio que donat un mon retorna un mon i un char. De forma inversa, la funcio myPutChar retorna un mon i un buit donats un mon i un char. D’aquesta manera podem pensar que les funcions d’entrada i sortida son funcions que modifiquen el mon. Aixi, podem simular una execucio en que llegim un char c1 i un altre c2 i generem un mon w3 en el que hi posem el char c1. A partir d’aquest mon generem un altre on tambe hi posem el segon char c2.

Si canviem una mica el format en que escribim aixo, es veu mes clar el que pasa. Abans, farem que l’estructura World sigui instancio de Monad i el tipus IO es una transformacio d’un mon a un altre.

type IO a = World -> (World, a)
getChar :: IO Char
putChar :: Char -> IO ()
main :: IO ()
main =
    getChar >>= \c1 ->
    getChar >>= \c2 ->
    putChar c1 >>
    putChar c2

Encara mes clar, podem convertir el operador bind o >>= fent servir la notacio do:

main = do
    c1 <- getChar
    c2 <- getChar
    putChar c1
    putChar c2

Ara ja sabem que es el que pasa realment, i podem imaginar que, d’alguna manera, el sistema operatiu i la implementacio de haskell s’encarreguen de garantir que les funcions getChar i similars funcionin adecuadament. Realment, segueix sent un llenguatge declaratiu.

Exercicis proposats:

P87974.hs

main :: IO ()
main = do
  nom <- getLine
  let s = saludaAdeu nom
  putStrLn s

saludaAdeu :: String -> String
saludaAdeu [] = ""
saludaAdeu (x : _)
  | x == 'A' = "Hello!"
  | x == 'a' = "Hello!"
  | otherwise = "Bye!"

P87082.hs

-- implementacio llegint per linea
main :: IO ()
main = do
    linea <- getLine
    let paraules = words linea
    let nom = paraules !! 0
    if nom /= "*" then do
        let imcCalculat = imc (read (paraules !! 1) :: Float) (read (paraules !! 2) :: Float)
        let resultat = imcAvaluarResultat imcCalculat
        putStrLn $ nom ++ ": " ++ resultat
        main
    else 
        return ()


-- funcio de IMC, donats dos floats saber el imc
imc :: Float ->  Float -> Float
imc p a = p / (a*a)

-- funcio de avaluacio, donat l'IMC saber l'string que identifica el resultat
imcAvaluarResultat :: Float -> String
imcAvaluarResultat x
    | x < 18 = "underweight"
    | x < 25 = "normal weight"
    | x < 30 = "overweight"
    | x < 40 = "obese"
    | otherwise = "severely obese"

---

Examens passats resolts

P48366

1. Evaluació d’expressions postfix (eval1 i eval1’)

eval1 :: String -> Int
eval1 s = eval1' [] (words s)

eval1' :: [Int] -> [String] -> Int
eval1' (x:_) [] = x
eval1' xs (y:ys)
    | y == "+" = eval1' ([((xs !! 0) + (xs !! 1))] ++ (tail $ tail xs)) ys
    | y == "-" = eval1' ([((xs !! 1) - (xs !! 0))] ++ (tail $ tail xs)) ys
    | y == "*" = eval1' ([((xs !! 0) * (xs !! 1))] ++ (tail $ tail xs)) ys
    | y == "/" = eval1' ([(div (xs !! 1) (xs !! 0))] ++ (tail $ tail xs)) ys
    | otherwise = eval1' ([(read y :: Int)] ++ xs) ys

Aquest codi implementa l’avaluació d’expressions en notació postfix utilitzant una pila com a llista. eval1 pren una cadena en notació postfix i la divideix en paraules utilitzant words s. Llavors, crida eval1' amb una pila buida i la llista de paraules. eval1' és una funció auxiliar que pren la pila actual xs i la llista de paraules restants ys.

• Si ys està buida, retorna el valor a la part superior de la pila com a resultat.
• Si la primera paraula en ys és un operador (+, -, *, /), desapila els dos elements superiors de la pila, realitza l’operació corresponent i torna a apilar el resultat.
• Si la primera paraula és un valor, el converteix en un enter i el puja a la pila.

2. Avaluació d’expressions postfix sense recursió (eval2)

eval2 :: String -> Int
eval2 s = head $ foldl operador [] (words s)
  where
    operador (x:y:ys) "+" = (y + x) : ys
    operador (x:y:ys) "-" = (y - x) : ys
    operador (x:y:ys) "*" = (y * x) : ys
    operador (x:y:ys) "/" = (y `div` x) : ys
    operador pila n = read n : pila

Aquesta funció realitza la mateixa tasca d’avaluació d’expressions postfix, però ho fa sense utilitzar la recursió. Utilitza la funció foldl per recórrer la llista de paraules i una pila. L’operador operador processa les operacions i valors, mantenint una pila actualitzada. La funció head retorna l’únic valor que queda a la pila al final, que és el resultat de l’expressió.

3. Funció fsmap

fsmap :: a -> [a -> a] -> a
fsmap x fs = foldl (\acc f -> f acc) x fs

Aquesta funció pren un element x de tipus a i una llista de funcions fs de tipus a -> a. La funció fsmap aplica totes les funcions de la llista fs a l’element x d’esquerra a dreta utilitzant foldl. En altres paraules, aplica cada funció de la llista fs successivament a l’element x, utilitzant el resultat anterior com a entrada per a la següent funció.

4. Divide and Conquer

divideNconquer :: (a -> Maybe b) -> (a -> (a, a)) -> (a -> (a, a) -> (b, b) -> b) -> a -> b
divideNconquer base divide conquer x = ...

qBase :: [Int] -> Maybe [Int]
qBase [] = Just []
qBase [x] = Just [x]
qBase xs = Nothing

qDivide :: [Int] -> ([Int], [Int])
qDivide [] = ([], [])
qDivide [x] = ([x], [])
qDivide (x:xs) = (filter (< x) xs, filter (>= x) xs)

qConquer :: [Int] -> ([Int], [Int]) -> ([Int], [Int]) -> [Int]
qConquer (x:_) _ (xs1, xs2) = (xs1 ++ [x] ++ xs2)

quickSort :: [Int] -> [Int]
quickSort v = divideNconquer (qBase) (qDivide) (qConquer) v

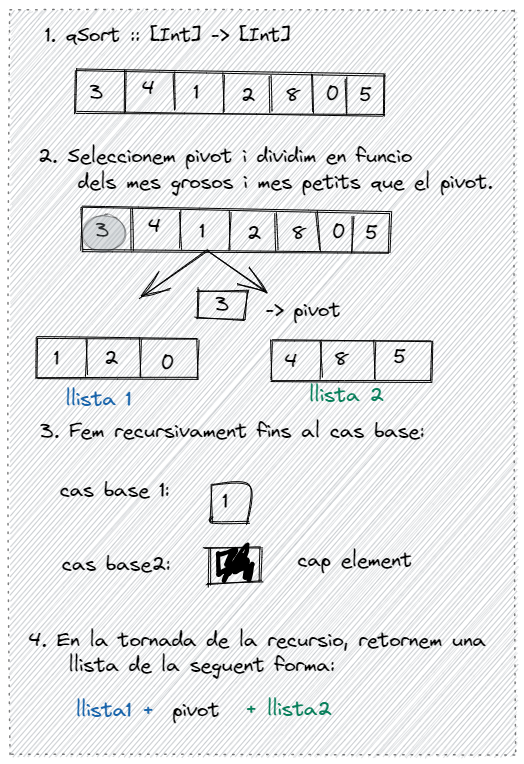
Aquestes funcions estan relacionades amb l’algorisme de QuickSort. La funció divideNconquer implementa la lògica de dividir i conquerir, utilitzant una funció base per a la condició de parada, una funció divide per a la divisió de la llista i una funció conquer per a la combinació dels resultats de les crides recursives. En aquest cas, es tracta de l’ordre de les funcions i l’ús d’una llista d’enters.

5. Definició del tipus Racional

data Racional = Racional Integer Integer

instance Show Racional where
    show (Racional n d) = (show (div n denComu)) ++ "/" ++ (show (div d denComu))
        where
            denComu = gcd n d

instance Eq Racional where
    (Racional n1 d1) == (Racional n2 d2) = n1 * d2 == n2 * d1

racional :: Integer -> Integer -> Racional
racional n d = (Racional (div n denComu) (div d denComu))
    where
        denComu = gcd n d

numerador :: Racional -> Integer
numerador (Racional n d) = n

denominador :: Racional -> Integer
denominador (Racional n d) = d

Aquesta part defineix un tipus Racional que representa números racionals. S’implementa una instància Show per mostrar-los com una fracció reduïda, una instància Eq per comparar-los i algunes funcions auxiliars com racional per crear racionals a partir del numerador i denominador, i les funcions numerador i denominador per obtenir-los.

6. Arbres de Calkin (arbres i llistes)

data Tree a = Node a (Tree a) (Tree a)

recXnivells :: Tree a -> [a]
recXnivells t = recXnivells' [t]
    where recXnivells' ((Node x fe fd):ts) = x:recXnivells' (ts ++ [fe, fd])

En aquesta part, es defineix un tipus d’arbre genèric Tree a que conté nodes amb valors de tipus a. La funció recXnivells recorre l’arbre per nivells, començant pel node arrel, i retorna una llista amb els elements de l’arbre en l’ordre en què es troben a cada nivell.

racionals :: [Racional]
racionals = recXnivells (arbreCalkin 1 1)

arbreCalkin :: Integer -> Integer -> Tree Racional
arbreCalkin a b = Node ra l r
    where
        ra = racional a b
        l = arbreCalkin a (a + b)
        r = arbreCalkin (a + b) b

En aquesta part, es crea una llista de racionals racionals utilitzant l’arbre arbreCalkin. Aquest arbre és una representació de la seqüència de racionals de Calkin, que es construeix mitjançant fraccions reduïdes. La funció recXnivells s’aplica a l’arbre per obtenir una llista dels racionals en ordre.

P91910.hs

data Expr a
    = Val a
    | Var String
    | Sum (Expr a) (Expr a)
    | Sub (Expr a) (Expr a)
    | Mul (Expr a) (Expr a)
    deriving Show


eval :: (Num a) => SymTab a -> Expr a -> Maybe a
eval symTab (Var s) = get symTab s
eval symTab (Val x) = Just x

eval symTab (Sum a1 a2) = (+) <$> (eval symTab a1) <*> (eval symTab a2)
eval symTab (Sub a1 a2) = (-) <$> (eval symTab a1) <*> (eval symTab a2)
eval symTab (Mul a1 a2) = (*) <$> (eval symTab a1) <*> (eval symTab a2)

CHAT-GPT:

En Haskell, Maybe és un tipus que representa la possibilitat de tenir un valor (Just a) o no tenir-lo (Nothing). Per realitzar operacions amb valors dins de Maybe, has de tractar aquest context de manera segura.

• <$> és un operador de fmap que et permet aplicar una funció a un valor dins d’un context Maybe (Just). Per exemple, pots usar fmap o <$> per aplicar una funció a un valor dins d’un Maybe, i si el valor és Nothing, la funció no s’aplica i s’obté Nothing.

• <*> és un operador d’aplicació que pren una funció continguda en un context Maybe i un valor contingut en un context Maybe i aplica la funció al valor si tots dos són Just. Si qualsevol d’ells és Nothing, el resultat és Nothing.

En el cas del teu codi, estàs treballant amb valors dins de Maybe quan avalues expressions. Per realitzar operacions aritmètiques (com la suma, la resta i la multiplicació), necessites aplicar aquestes operacions de manera segura als valors continguts en Maybe. Aquí és on <$> i <*> són útils:

• <$> s’utilitza per aplicar les operacions de manera segura als valors continguts en Maybe, si tots dos són Just. Si un d’ells és Nothing, el resultat és Nothing.

• <*> s’utilitza per aplicar funcions als valors continguts en Maybe de manera segura, novament si tots dos són Just. Si un és Nothing, el resultat és Nothing.

Aquests operadors permeten treballar amb els valors continguts en Maybe de forma segura i expressiva, sense necessitat de comprovar manualment si els valors són Just o Nothing.

Tambe es pot fer servir la funcio liftM2 que donades dos monades i una funcio:

• extreu el valor de dins de les dues monades

• aplica la funcio a els valors extrets

• encapsula el resultat en una nova monada La funcio liftM2 s’ha d’importa (import Control.Monad) o es pot definir de la seguent manera:

  -- liftM2 :: Monad m => (a -> a -> a) -> m a -> m a -> m a
  liftM2 f x y = do
    vx <- x
    vy <- y
    return $ f vx vy